线性插值法
目录
线性插值法是指使用连接两个
假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的值。根据图中所示,我们得到两点式直线方程:
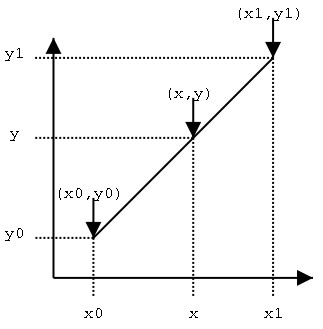
假设方程两边的值为α,那么这个值就是插值系数—从x0到x的距离与从x0到x1距离的比值。由于x值已知,所以可以从公式得到α的值
同样
这样,在代数上就可以表示成为:y = (1 − α)y0 + αy1或者,y = y0 + α(y1 − y0)
这样通过α就可以直接得到 y。实际上,即使x不在x0到x1之间并且α也不是介于0到1之间,这个公式也是成立的。在这种情况下,这种方法叫作线性外插—参见 外插值。
已知y求x的过程与以上过程相同,只是x与y要进行交换。
线性插值近似法
线性插值经常用于已知函数f在两点的值要近似获得其它点数值的方法,这种近似方法的误线定义为
RT = f(x) − ρ(x)
其中ρ表示上面定义的线性插值多项式
根据
线性插值法是认为现象的变化发展是线性的、均匀的,所以可利用两点式的直线方程式进行线性插值。
两点式的直线方程式为:
式中 X0,Y0,X1,Y1——已知的统计数据;
X——X0,X1之间的任何数据;
Y——与X对应的插值数据。
例 某地区居民货币收入和消费支出情况如表1所示。试推算该地区居民收入为19.5亿元时,其相应的消费支出是多少?
表1 居民货币收入和消费支出资料(单位:亿元)
| 顺序 | 货币收入(x) | 消费支出(y) |
| 0 | 18.2 | 15.8 |
| 1 | 19.8 | 17.2 |
解:
= 16.9
所以,当该地区居民收入是19.5亿元时,其消费支出是16.9亿元。
由于线性插值法只利用两点的对应值宋推算两点之间的对应值,而两点对应值本身往往受到各种偶然因素的影响,所以线性插值结果可能误差较大。
附件列表
故事内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
